スポンサーリンク
確率の定義
これは定義なのでしっかり暗記します。
※場合の数があやふやな人は、場合の数をきっちり固めてから確率の勉強に入りましょう
例
- サイコロを１つ投げて、１の目がでる確率は
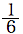
- サイコロを１つ投げて、偶数（２，４，６）の目がでる確率は
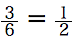
- サイコロを１つ投げて、6以下の目が出る確率１（必ず起こる確率は１）
- サイコロを１つ投げて、10の目が出る確率０（絶対に起こらない確率は０）
和の法則
基礎例題１
- （１） 出た目の和が６になる確率を求めなさい。
- （２） 出た目の和が12になる確率を求めなさい。
- （３） 出た目の和が６の倍数になる確率を求めなさい。
解答
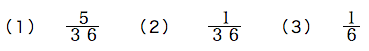
(1)解説
すべての場合の数は、６×６＝36（通り）です。
和が６になる場合をすべて書き出します。
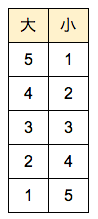
上記の５通りなので、
です。
(2)解説
和が12になる場合をすべて書き出します。
|
大 |
小 |
|
6 |
6 |
上記の１通りなので、
です。
(3)解説
和が６の倍数になるのは、６のときと12のときしかないので、確率の定義通り考えると
もちろん約分して答えは
です。
これは、別の見方もあり、和が６になる確率と和が12になる確率の和
として答えを出すこともできます。
２つの目の和が６または12のとき、のように独立した事象のどちらかが起こる確率は、それぞれの確率の和をとることで求まります。
積の法則
基礎例題２
１を2回続けて引く確率を求めなさい。
解答
解説
連続して起こる事象の確率はかけ算をします。
いわゆる積の法則です。
４枚の中から1枚の１を引く確率は
なので、
答えはとなります。
「場合の数」で学習をした樹形図です。
連続して試行すると、全場合の数が爆発的ひろがっていく樹形図のイメージです。かけ算ですね。
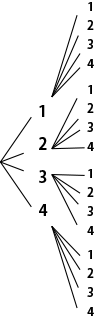
連続して起こる事象の確率は、確率どうしのかけ算となるということをきっちり覚えましょう。
※ここでは、長々とした数学的厳密性のある説明はしません。その方が有益と考える為、上記のような感覚的な説明に留めておきます。
余事象
ここでは場合の数でも学習した余事象について学びます。
基礎例題3
取り出した玉はもとに戻しません。少なくとも１個白玉の確率はいくらですか。
解答
解説
「少なくとも１個白玉」とは白玉の個数は1個でも２個でも３個全部でも良いのだから、非常にたくさんの場合分けが必要です。
- （白白白）
- （白白赤）
- （白赤白）
- （赤白白）
- （白赤赤）
- （赤白赤）
- （赤赤白）
全７パターンの場合分けとなります。こういうときは余事象でしたね。
すべて赤玉の確率は
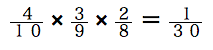となります。よって、全事象の確率である１から引いて
となり答えはとなります。同時に取り出す
基礎例題４
- （１）取り出した２つが、２つとも白玉である確率はいくらですか。
- （２）取り出した２つが、白玉１つ、赤玉1つである確率はいくらですか。
解答
「同時に取り出す」ときの公式の使い方がわかりません！という声が聞こえてきそうです。こういうときは、定義にしたがってきっちり考えるのです。
(1)解説
白玉どうし、赤玉どうしを区別するために名前をつけます。
- 白:Ｗ Ｘ Ｙ Ｚ
- 赤:Ａ Ｂ Ｃ Ｄ Ｅ
全場合の数は、異なる９個から２個を取り出す組み合わせで
取り出した２つが、２つとも白玉である場合の数は、Ｗ、Ｘ、Ｙ、Ｚの４個から２個を取り出す組み合わせで
よって
答えは
となります。
ポイント
答えは求まりましたが、「同時に取り出す」と「同時ではなく１つ１つ順番に取り出す」の違いを見ておきましょう。
1つ１つ順番に取り出すルールで、２つとも白玉である確率はいくらなのでしょうか。
1つ目が白の確率と、２つ目が白の確率の積で求まります。
同じ答えです。
実はこれは偶然ではありません。
常に同じ確率です。だから、積の法則で答えを出しても大丈夫なのです。
その結果を右手の玉から見ても左手の玉から見ても白、白という結果で、区別はできません。これが先の答えが同じになる理由です。
何を言っているのかよくわからないですか？
頭がこんがらがるのが普通なので、あせらずよく考えて理解しましょう！
しかし、どうしても腑に落ちないなら「同時に取り出す」という問題文通りに答えが出せればそれで大丈夫です。
(2)解説
この問題では1つ１つ順番に取り出すルールと、同時に取り出すルールの違いが如実に現れます。
以下に2つの解法を示します。
自分にとってしっくりくる解法を選んでいただければ大丈夫です。
①同時に取り出した という問題文通りの解き方
全場合の数は、異なる９個から２個を取り出す組み合わせで
取り出した２つが、１つ白玉、１つ赤玉である場合の数は
５Ｃ１×４Ｃ１＝５×４＝20（通り）
よって答えは
②１つ１つ順番に取り出す計算方法での解き方
「同時に取り出した２つが、白玉１つ、赤玉1つである確率」とは
「1つ目が白玉、2つ目が赤玉の確率」と「1つ目が赤玉、2つ目が白玉の確率」の和になります。
1つ目が白玉、2つ目が赤玉の確率
1つ目が赤玉、2つ目が白玉の確率
これらの確率の和をとって
当然ですが、２つの解法で同じ答えがでてきますね。
その際は「取り出した２つが２つとも赤玉である確率」を求めて、全確率１からこれと（１）の答えを引きます。
これで確率の基礎は大丈夫です！！
