スポンサーリンク
公式
まずは二つの公式を載せます。
順列
異なるn個のものからr個選び、並べる これを【 順列 】といいその総数は
![]()
組合せ
異なるn個のものからr個選ぶ これを【 組合せ 】といいその総数は
![]()
※r!=r×(r-1)×(r-2)×・・・×3×2×1
ポイント
そのためには「全パターンを書き出す」ことからはじまります。
以下のような姿勢で問題に臨みましょう。
- 書き出しをすることで問題の全容を把握する
- 公式の正しい使い道が見える
- 結局は、全部書き出さなくとも、計算で答えがでる
しかし、次のようなパターンもあります。
- 書き出しをすることで問題の全容を把握する
- 公式が適用できないことがわかる。最後まで書き出しきるのみ
書き出し
基礎例題①
解答と解説
『えーと、どっちの公式を使うんですか。』と考えずに、とにかく書き出しましょう。
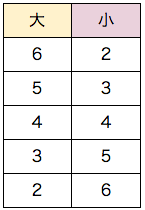
以上の5通りです。
小さい順、大きい順、あいうえお順などのように、書き出しの際はルールを決めます。
書き出しきってそれで終わりました。
このようにそもそも公式なんて通用しない問題もあります。まず、これを知っておいてください。
基礎例題②
解答と解説
これも書き出しで求めます。順列でも組合せでもありません。
決められた大きさ(1200円)を埋める問題は、まず大きいもの(500円)で埋めます。残りの隙間を小さいもので埋めるのは簡単です。
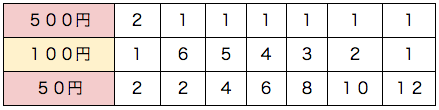
順列
いよいよ順列の公式が使えるケースがどのような場合なのかを見ていきましょう。
まずは書き出しをすることで公式の仕組みを理解しましょう。
基礎例題③
解答と解説
まずは小さい順に書き出してみます。
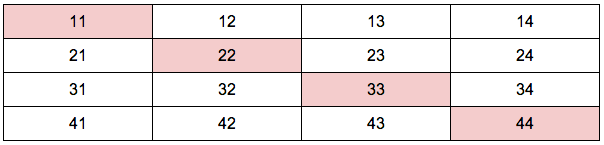
赤い背景部分はつくれません。同じ数字のカードが2枚ないからです。
よって、12通りになります。
基礎例題④
解答と解説
小さい順に書き出します。
123 124 125 132 134・・・ 何回も百の位の1を書くのは嫌になっちゃいます。以下のような書き方で省略しましょう。木の枝分かれのような図なので、樹形図といいます。
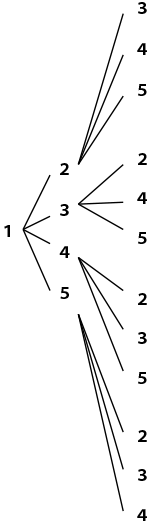
これはもしかして、百の位が 2 のときも、3 のときも・・・5通りすべてで12通りずつ作れますね!
12×5=60通り 枝分かれする順にかけ算をかくと 5×4×3=60通り
この計算、5×4×3=60 が、冒頭に出て来た順列の公式そのものとなります。
異なるn個のものからr個選び、並べる
![]()
本問においては、異なる5個( n )のものから3個( r )選び、並べる。ということですね。
順列の公式は条件付き問題になったとたん、使い方が分からなくなる人が多いです。公式丸暗記では今後対応しきれません。
上記の仕組みをきっちり理解してください!
全場合の数がどんな樹形図になるのか明確なイメージがわけば、どんなかけ算をすればよいのか自明になります。
※ここをきっちりと理解しておけば、確率の理解がスムーズになります。
基礎例題⑤
解答と解説
樹形図の全体像をイメージしましょう。(実際に書いてみるのもよいです。)規則正しく枝分かれしていきますね。
そのイメージがあれば、計算1発ですね。
6×5×4×3×2×1=720(通り)
答え 720通り
条件つき問題
条件がある場合、そこから決めていくことで効率よく調べきることができます。
基礎例題⑥
解答と解説
異なる4枚から3枚を取り出して並べる、まさに順列の問題です。
しかし、【 0 】は、はじめ(百の位)におけない という条件が隠れています。
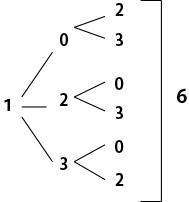
百の位が 2、3 のときも同様に6通りずつあるので、
6×3=18通りとなります
基礎例題⑦
両端が男子になる並び方は何通りありますか。
解答と解説
男子をA、B・女子をP、Q、Rとします。
男子の並び方は
A○○○B と B○○○A の2通りあります。
女子は○○○のところに並べます。
女子の並べ方は
3×2×1=6(通り)※順列ですね
よって、2×6=12(通り)
答えは12通りとなります。
この式【 2×6=12 】ですが、なぜかけ算なのか分からなくなった人はいませんか?
これも、樹形図の枝分かれだからです。A○○○B と B○○○A の2通りにそれぞれ6通りずつ枝分かれがあるからです。
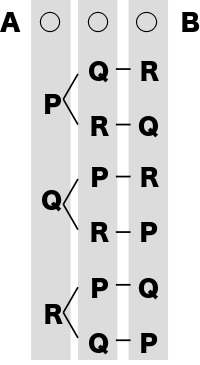
組合せ
場合の数における最重要項目です。
基礎例題⑧
解答と解説
順列との違いがわかりますか?
「2人を選ぶ」と、「2人を選んで並べる」の違いです。
この問題で聞かれているのは、「2人を選ぶ」です。
「2人を選ぶ」と、「2人を選んで並べる」の2つですが、より簡単に求められるのは「2人を選んで並べる」順列の方です。
4×3=12通りですね。
この12通りの中には、
- PQ
- QP
という2通りが含まれていますが、組合せにおいてはこの2通りは同じものとみなします。
2人を選ぶだけで、並び方は関係がないからです。
同じものを2回数えてしまっているので、
12÷2=6
6通り が答えです。
順列 ÷ 重複 = 組合せ ・・・これが組合せの公式の意味です。
※組合せを求める状況で、条件付き順列を考慮することは一切ないので安心してください。
公式を用いて、上記の解き方を簡潔にかくと
![]() となります。
となります。
基礎例題⑨
A、B、C、D、Eの5人の中からそうじ当番を3人選ぶ選び方は全部で何通りありますか。
解答と解説
「3人を選ぶ」と、「3人を選んで並べる」 の違いはもう大丈夫でしょうか。
より簡単に求められる方が、「3つを選んで並べる」ですね(いわゆる順列)。
5×4×3=60通りです。
この60通りの中には
- ABC
- ACB
- BAC
- BCA
- CAB
- CBA
が含まれています。
この6つは「3人を選ぶ」だけのときは、同じものとみなします。(並べ方は関係ないからです)。
つまり、6回重複して数えて、60通りだったのですから、
60 ÷ 6 = 10 で組合せが求まります。
答え 10通り となります。
公式を用いて、上記の解き方を簡潔にかくと
![]() となります。
となります。
組み合わせ公式の確認
異なるn個のものからr個選ぶ事を組合せといい、その総数は
![]()
※r!=r×(r-1)×(r-2)×・・・×3×2×1・・・この分母が重複の数ですね!
別解 組合せの重要公式
5人からそうじ当番を3人選ぶと、自動的に2人が選ばれないことになります。
つまり、このそうじをしなくてもよい2人を選べば、そうじ当番3人も決まるのです。
よって、5人からそうじをしなくてもよい2人を選べばよいので
答え 10通りとなります。
5C3=5C5-3 なのです。
基礎例題⑩
黒石6個と、白石4個を1列に並べます。並べ方は全部で何通りありますか。
解答と解説
並べるという言葉で、一見順列のようだが・・・実は組合せなんですね。
理屈をしっかり理解・暗記しましょう。
黒石と白石の並べ方の1例をかいてみます。
![]()
白石を1,5,7,8、に 置きました。
つまり、4個の白石を置く場所を1~10の中から4つ選んだのです。これは組合せですね。
![]()
答え210通りとなります。
もちろん、10C6=10C4 です。
余事象
基礎例題⑪
解答と解説

上で示した通り、4パターンの場合分けがあります。
積が偶数になる3パターンがそれぞれ何通りずつあるのかを求めて足すことで答えがでます。しかし目の出方は全部で、6×6=36通りあり、そこから積が奇数になる場合の数を引いた方が楽ですね。
このように、求めたい事象ではない方を余事象といいます。
大小どちらも奇数の目が出るのは、
3×3=9(通り)なので、36-9=27(通り)
答え27通りです。
基礎例題⑫
少なくとも1人男子を選ぶ選び方は何通りありますか。
解答と解説
少なくとも1人男子とは、
- 【男 女 女】
- 【男 男 女】
- 【男 男 男】
のどれかです。3パターンの場合分けが必要ですね。
「少なくとも1人男子」の余事象は何になるでしょうか。
答えは「1人も男子がいない=全員女子」です。
「全事象」から、「全員女子」を引いて求めたほうが速いです。
全場合の数は、8人から3人選ぶ場合の数なので、
![]()
全員女子の場合の数は、女子5人の中から3人を選ぶ選び方なので
![]()
よって、56-10=46(通り)です。
以上で場合の数の基礎はばっちりです!!








