スポンサーリンク
例題１
箱の中に、２本の当たりくじと５本のはずれくじが入っている。このくじを2本同時に引く。
(1) 2本ともはずれくじを引く確率はいくらか。
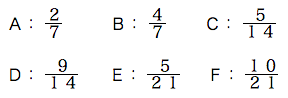
(2) 当たりくじとはずれくじを1本ずつ引く確率はいくらか。
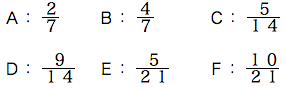
(1) 2本ともはずれくじを引く確率はいくらか。
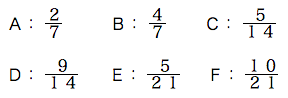
(2) 当たりくじとはずれくじを1本ずつ引く確率はいくらか。
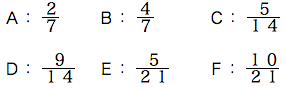
解答と解説
解答
(1)F
(2)F
(2)F
解説
当たりくじ2本をX，Y
はずれくじ５本をP、Q、R、S、Tと名付けます。
(1)解説
7つから2つを選ぶのが全事象で、
はずれくじ2本を引くのは、P、Q、R、S、Tから2本選ぶので、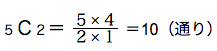
よって求める確率は
となり答えはFです。
※1本ずつ2回続けて引いて、どちらもはずれであった確率と等しいので、それで求めてもかまいません。
(2)解説
当たりくじ1本を引くのはX，Yから1つ選ぶので２通り、
はずれくじ1本を引くのは、P、Q、R、S、Tから１本選ぶので５通り
よって、当たりくじ1本、はずれくじ1本を引くのは、２×５＝10（通り）
よって、求める確率はとなり答えはFです。
- 1本ずつ2回続けて引いて、「当たり、はずれ」となった確率と「はずれ、当たり」となった確率の和を求めてもかまいません。
- 2本とも当たりの確率を求めて、余事象で解いてもかまいません。
例題２
大小2つのサイコロを同時に投げます。
(1) 2つのサイコロの目の積が偶数になる確率はいくらか。
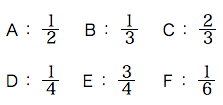
(2) 2つのサイコロの目の和が９以下になる確率はいくらか。
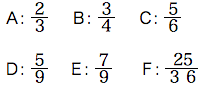
解答と解説
解答
（１）E
（２）C
（２）C
(1)解説
目の出方は4パターンである。どちらも奇数の目がでた場合の余事象を求めればよい。
どちらも奇数の目が出る確率は
なので
となり、答えはEです。
(2)解説
目の和が10,11,12の場合の余事象を求めます。
※目の和は１＋１＝２ から ６＋６＝12まであります。2から９までの8通り調べるのは嫌ですね。
- 目の和が10になるのは （大、小）＝（６、４）・（５、５）・（４、６）の３通り
- 目の和が11になるのは （大、小）＝（６、５）・（５、６）の２通り
- 目の和が12になるのは （大、小）＝（６、６）の１通り
以上より目の和が10以上になるのは、３＋２＋１＝６（通り）あるので、
目の和が10以上になる確率は
となります。
よって求める確率は
答えはCです。
