スポンサーリンク
例題1
ある大学で150人の学生を対象に、通学時の電車とバスの利用状況についてアンケートを取った。
その結果電車を利用している学生は122人、バスを利用している学生は31人いた。
また、電車とバスの両方を利用している学生は12人であった。
このとき、電車とバスを両方とも利用していない学生は何人か。
その結果電車を利用している学生は122人、バスを利用している学生は31人いた。
また、電車とバスの両方を利用している学生は12人であった。
このとき、電車とバスを両方とも利用していない学生は何人か。
A:9人 B:11人 C:13人 D:15人
E:16人 F:18人 G:20人 H:22人
解答と解説
解答
A
解説
このようなタイプの出題にはベン図です。
ベン図に情報を入れるとき、重なっている箇所から入れていきます。
まず、イ=12(人)です。
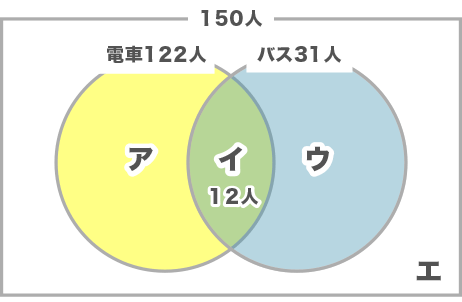
ア:122-12=110(人)
ウ:31-12=19(人)
エ:150-(110+12+19)=9(人)
よって答えはAです。
※ア+イ+ウの求め方は、122+31-12=141(人)が最もよく使われています。
例題2
ある中学校の男子生徒は230人、女子は生徒は220人です。
この中学校でメガネをしている生徒は203人です。メガネをしていない女子生徒が122人のとき、メガネをしている男子生徒は何人いますか。
A:85人 B:95人 C:102人 D:105人
E:110人 F:112人 G:125人 H:127人
この中学校でメガネをしている生徒は203人です。メガネをしていない女子生徒が122人のとき、メガネをしている男子生徒は何人いますか。
A:85人 B:95人 C:102人 D:105人
E:110人 F:112人 G:125人 H:127人
解答と解説
解答
D
ベン図をかいてみましょう。かけない・・・ですか?
かけないことはないのですが、違和感があります。
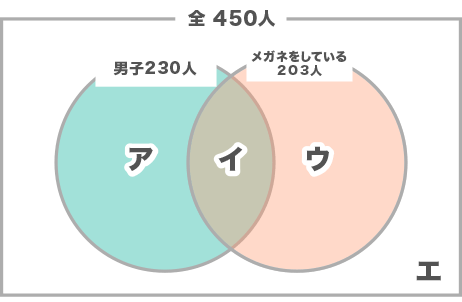
メガネをしていない女子生徒はエなので、エ=122(人)です。
ウ:220-122=98(人)・・・ウ+エが女子220人なので
イ:203-98=105(人)
よって答えはDです。
この問題はベン図よりも、表の方がしっくりきますね。
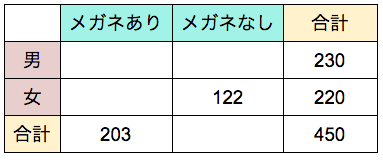
メガネをしている女子は 220-122=98(人)
メガネをしている男子は 203-98=105(人)
よって答えはDです。
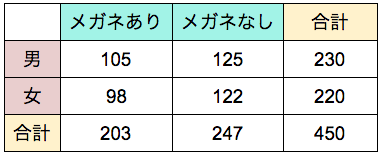
答えはでましたが、表の残りの部分もうめておきましょう。
例題3
48人の小学生に、ピーマン、ナス、セロリについて、好きか嫌いかのアンケートをとったところ、次のような結果になった。
- ピーマンが嫌い:20人
- ナスが嫌い:18人
- セロリが嫌い:13人
- ピーマンとナスが嫌い:12人
- ナスは好きだが、ピーマンとセロリが嫌い:5人
- ピーマンとナスは好きだが、セロリが嫌い:2人
- 3種類すべて嫌い:5人
- このとき、3種類とも好きな小学生は何人いますか。
A:3人 B:5人 C:8人 D:10人
E:13人 F:15人 G:17人 H:20人
解答と解説
解答
H
解説
ベン図は3重までならオーケーです。
4重以上の情報はベン図ではまとめられません。
4重以上の情報はベン図ではまとめられません。
ではそのときは、どうするのか。
4重の情報は難しすぎるため、おそらくSPIでは出題されません。いらぬ心配です。
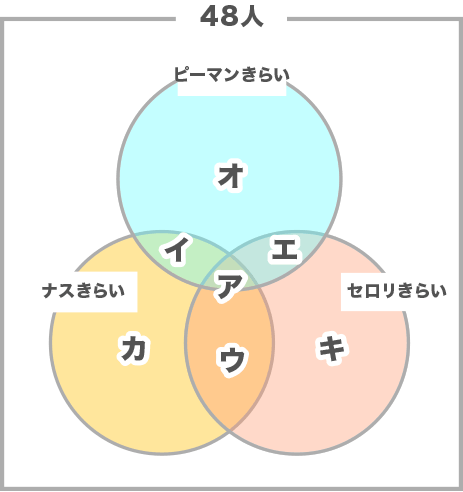
まずは重なっている箇所から入れていきます。
- 3種類すべて嫌い:5人⇒ アに入ります
- ピーマンとナスが嫌い:12人⇒ アとイの合計
よってイ=7人
- ナスは好きだが、ピーマンとセロリが嫌い:5人⇒ エに入ります
- ピーマンとナスは好きだが、セロリが嫌い:2人⇒ キに入ります
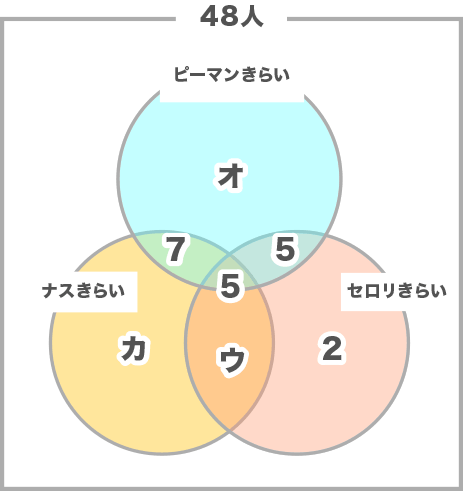
さらに下記を用いて残りをうめます。
- ピーマンが嫌い:20人
- ナスが嫌い:18人
- セロリが嫌い:13人
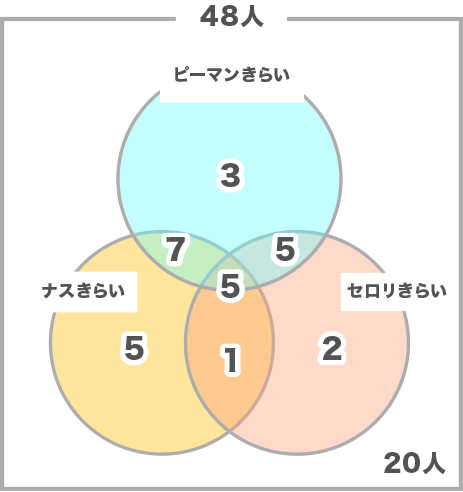
全48人から、輪の中に入った28人を引いた、残り20人が求める答えです。








