スポンサーリンク
練習問題1
(1)両科目ともに70点以上だった生徒が18人だとすれば、両科目ともに70点未満だった生徒は何人いますか。
A:2人 B:4人 C:5人
D:7人 E:8人 F:9人
(2)両科目とも70点以上だった生徒は何人以上何人以下ですか。
A:4人以上20人以下 B:4人以上22人以下
C:7人以上20人以下 D:7人以上22人以下
E:10人以上20人以下 F:10人以上22人以下
G:14人以上20人以下 H:14人以上22人以下
解答
(2)H
(1)
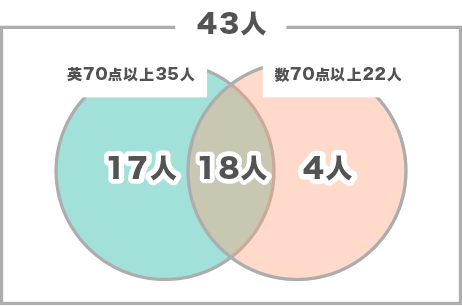
このようにベン図にまとめられます。
43-(17+18+4)=4(人)
答えはBです。
(2)
範囲は、ベン図でも解けますが、線分図で解くのがおすすめです。
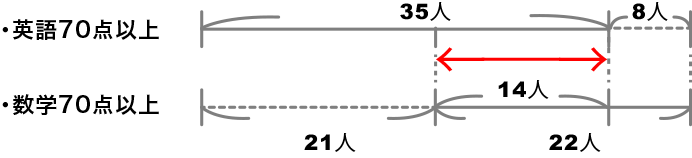
重なりを最も少なくすると上図のようになります。最小は14人です。
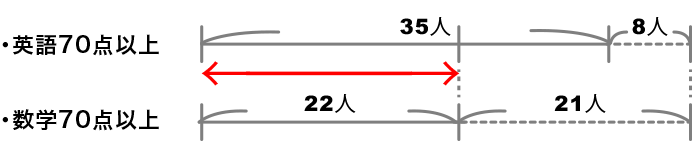
重なりを最大にすると、上図のようになります。最大が22人は明らかです。
答えはHです。
練習問題2
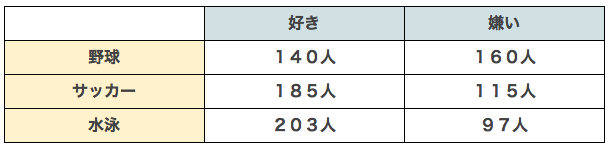
(1)野球もサッカーも好きという人が88人いた。野球もサッカーも嫌いな人は何人いますか。
A:35人 B:40人 C:43人 D:49人
E:55人 F:63人 G:67人 H:69人
(2)野球が嫌いな人のうち、145人は水泳が好きだという。野球と水泳の両方が好きな何人いますか。
A:47人 B:58人 C:67人 D:75人
E:90人 F:104人 G:113人 H:122人
(3)サッカーも水泳も好きな人が114人、そのうち3つとも好きな人は26人いるという。この3つが嫌いな人は何人いますか。
A:3人 B:6人 C:13人 D:17人
E:19人 F:22人 G:25人 H:31人
解答
(2)B
(3)B
(1)
野球とサッカーを、ベン図でまとめます。重なっている箇所、88人から入れて残りを計算します。
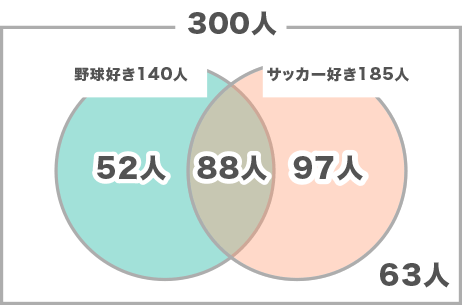
野球もサッカーも嫌いな人は、63人います。答えはFです。
(2)
野球と水泳を、ベン図でまとめます。
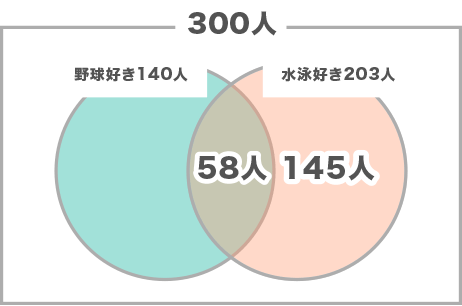
野球と水泳の両方が好きな人は、58人います。答えはBです。
(3)
3種目すべてをベン図にまとめます。(1)(2)までにわかったことも図に記入していきます。特に迷うことなく、すべてが埋まるでしょう。
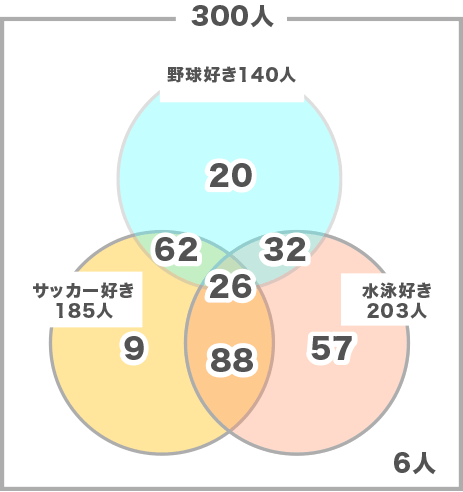
3種目すべてが嫌いな人は輪の中に入らなかった6人です。答えはBです。
練習問題3

このテストで1問だけ正解した人の人数が20人のとき、問2を正解した人は何人ですか。
A:20人 B:22人 C:25人 D:31人
E:34人 F:39人 G:41人 H:45人
解答と解説
解説
ベン図にまとめます。注意点は、得点が5点の学生17人がどこに入るかです。
下図のアとイの箇所に分かれて入ります。
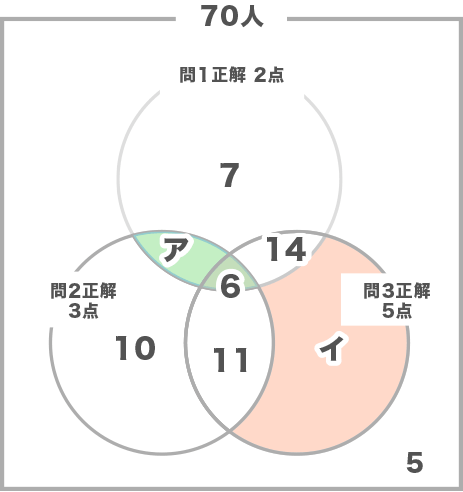
1問だけ正解した人20人に着目すると、7+10+イ=20 よりイ=3(人)
ア+イ=17(人)なので、ア=14(人)
よって、問2を正解した人数は、14+6+10+11=41(人)
答えはGです。








