スポンサーリンク
練習問題①
Ｐ、Ｑ、Ｒ、Ｓ、Ｔの５人がバトミントンのリーグ戦行った。5人の勝敗について次のことが分かっている。
- ＰはＱに勝ったが、Ｓに負けた。
- ＱはＲに勝ったが、残りは全敗した。
- ＴはＰとＲに勝ったが、全勝ではない。
- 引き分けはなかった。
(1)次のア、イ、ウの推論のうち、必ずしも誤りとはいえない推論はどれか。
- ア：３勝１敗は２人だ
- イ：２勝２敗は２人だ
- ウ：１勝３敗は３人だ
A：アだけ B：イだけ C：ウだけ D：アとイの両方
E：アとウの両方 F：イとウの両方 G：アとイとウのすべて
H：必ずしも誤りとは言えない推論はない
（２）更にどのような情報が追加されれば、全ての試合の勝敗が決まるか。ただし、情報として追加する選択肢は、できる限り抑えるものとする。
- カ：Ｐは1勝３敗だった
- キ：Rは２勝２敗だった
- ク：Sは３勝1敗だった
A：カだけ B：キだけ C：クだけ D：カとキの両方
E：カとクの両方 F：キとクの両方
G：カとキとクのすべて
H：カとキとクのすべてが追加されても分からない
解答と解説
解答
(1)E
(2)B
(2)B
まず確定していることを入れます。
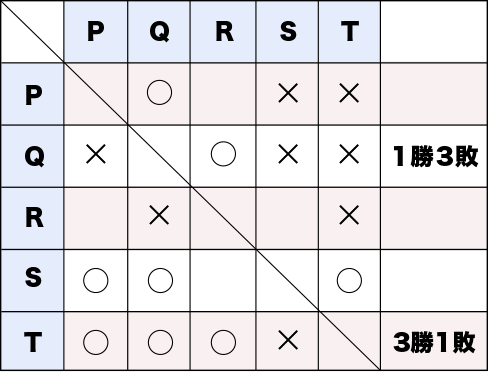
Ｔは全勝ではないため、Ｓに負けていることもわかります。
これを見ながら順に検証します。
(1)
ア：３勝１敗は２人だ
３勝１敗になりうるのはＳとＴで実際にそうなるように星取り表をうめることができる。
これは必ずしも誤りとはいえない。
イ：２勝２敗は２人だ
２勝２敗になりうるのはＰとＲだが、2人がともに２勝２敗になる星取り表はつくれません。PとRの対戦があるからです。
これは誤りである。
ウ：１勝３敗は３人だ
１勝３敗になりうるのはＰとＱとＲで実際にそうなるように星取り表をうめることができる。
これは必ずしも誤りとはいえない。
よって答えはＥです。
(2)
カ：Ｐは1勝３敗だった
ＲとＳの試合結果が決まらない。
キ：Rは２勝２敗だった
すべて確定する。
ク：Sは３勝1敗だった
ＰとＲの結果が決まらない。
よって答えはBです。
