スポンサーリンク
問題
- ① それぞれの玉が少なくとも1個入っている
- ② 赤玉の数は白玉より多い
(1)次のア、イ、ウの推論のうち、必ず正しいものはどれか。
- ア:赤玉が3個であれば、白玉は2個である
- イ:白玉が3個であれば、黒玉は1個である
- ウ:黒玉が2個であれば、赤玉は4個である
A:アだけ B:イだけ C:ウだけ D:アとイの両方
E:アとウの両方 F:イとウの両方
G:アとイとウのすべて H:必ず正しい推論はない
(2)次のカ、キ、クの推論のうち、必ず正しいものはどれか。
- カ:赤玉が3個以下であれば、黒玉は4個以上である
- キ:白玉の数が黒玉より多ければ、黒玉は1個である
- ク:白玉と黒玉の個数が同じであれば、赤玉は6個である
A:カだけ B:キだけ C:クだけ
D:カとキの両方 E:カとクの両方 F:キとクの両方
G:カとキとクのすべて H:必ず正しい推論はない
解答
(2)B
解説
順に検証していきます。
「必ず正しい」または、「必ずしも正しくはない」のどちらかを判定するとき
「必ず正しい」というためには、考えうるあらゆるパターンを書きだしそのすべてが正しいという必要があります。
そのため大事なのは全パターンの書き出しです。
逆に「必ずしも正しくはない」ことを示すためには、反例を1つでも挙げればそれでよいです。
反例がすぐに思いつけば、当然全パターンの書き出しをする必要はありません。
反例探しと全パターンの書き出しのどちらが速いのかは、問題次第としか言えません。全パターン書き出しを厭わない姿勢が必要です。
(1)
ア:赤玉が3個であれば、白玉は2個である

反例がある。これは必ずしも正しくない。
イ:白玉が3個であれば、黒玉は1個である
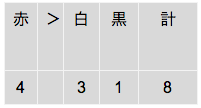
全パターンはこの1通りのみ。 この推論は必ず正しい。
ウ:黒玉が2個であれば、赤玉は4個である。
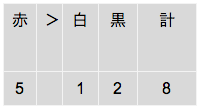
反例がある。これは必ずしも正しくない。
答えはBです。
(2)
カ:赤玉が3個以下であれば、黒玉は4個以上である
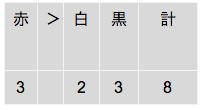
反例がある。これは必ずしも正しくない。
キ:白玉の数が黒玉より多ければ、黒玉は1個である

反例を作るために黒玉を2個にしてみると、合計が少なくとも9個以上ないといけないことがわかり反例が作れないことがわかる。
よってこれは必ず正しい。
ク:白玉と黒玉の個数が同じであれば、赤玉は6個である。

反例がある。これは必ずしも正しくない。
答えはBです。
別解
全パターンの書き出しをすると下の表のようになります。

これを見ながら検証していくことも良い解法です。








